Cách sử dụng GeoGebra để mô hình hóa khái niệm hình trụ

[ad_1]

Nội dung chính của bài viết này sẽ xoay quanh các bước hướng dẫn mô hình hóa khái niệm hình trụ bằng phần mềm GeoGebra.

Mình nói trước, đây là một bài viết nâng cao, vậy nên sẽ có rất nhiều thao tác với rất nhiều bước khác nhau => chính vì thế mà mình không thể hướng dẫn với các bạn chi tiết từng bước, từng bước như các bài trước đó được.

Vì vậy, trước khi đọc và làm theo bài hướng dẫn này thì bạn cần có các kiến thức về GeoGebra ở mức cơ bản trước đã, đặc biệt là biết cách vẽ hình trong không gian 3 chiều, tức trong phối cảnh 3D Graphics.

Bạn nên xem thêm 2 bài viết cơ bản này:

Ngoài ra thì trong bài viết này, mình cũng hướng dẫn thêm cho các bạn cách vẽ hình trụ trong không gian 3 chiều và trên mặt phẳng.

#1. Khái niệm hình trụ và ý tưởng sư phạm

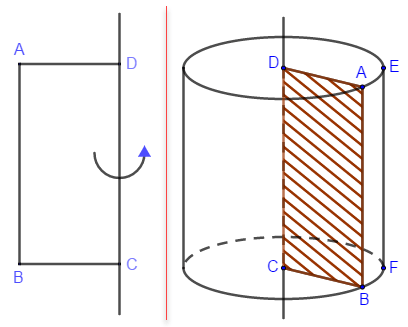
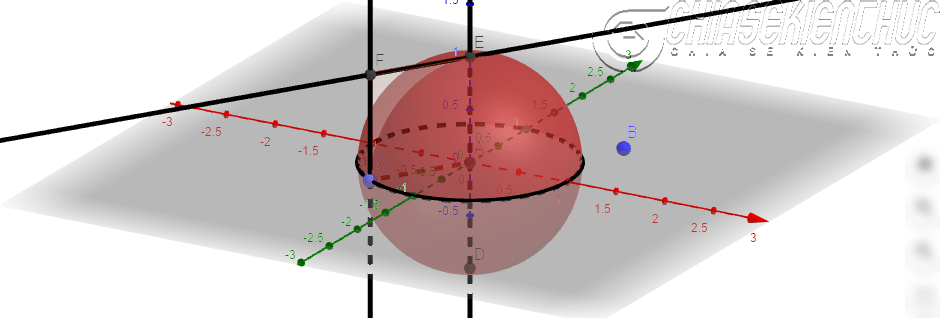
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ như hình bên dưới.

Ý tưởng sư phạm ở đây là chúng ta vẽ một hình chữ nhật => tạo vết cho nó => sau đó cho nó chuyển động xoay quanh một đường tròn. Khi hình chữ nhật chuyển động đủ một vòng thì vết của nó sẽ vẽ tạo ra một hình trụ, vậy thôi !

#2. Các bước mô hình hóa khái niệm hình trụ

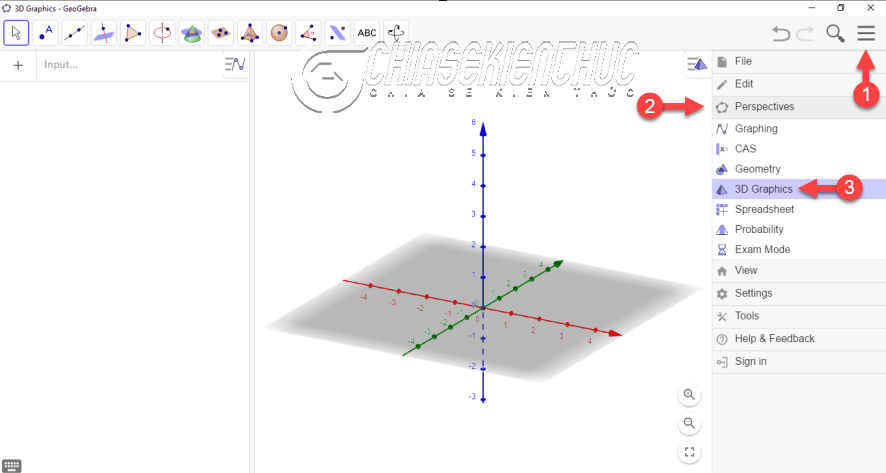
+ Bước 1: Đầu tiên, bạn hãy mở ngữ cảnh không gian 3 chiều để thực hiện các bước mô hình hóa.

Thực hiện: Khởi động phần mềm GeoGebra => chọn vào biểu tượng “trùng nhau” => chọn Perpectives => sau đó chọn 3D Graphics

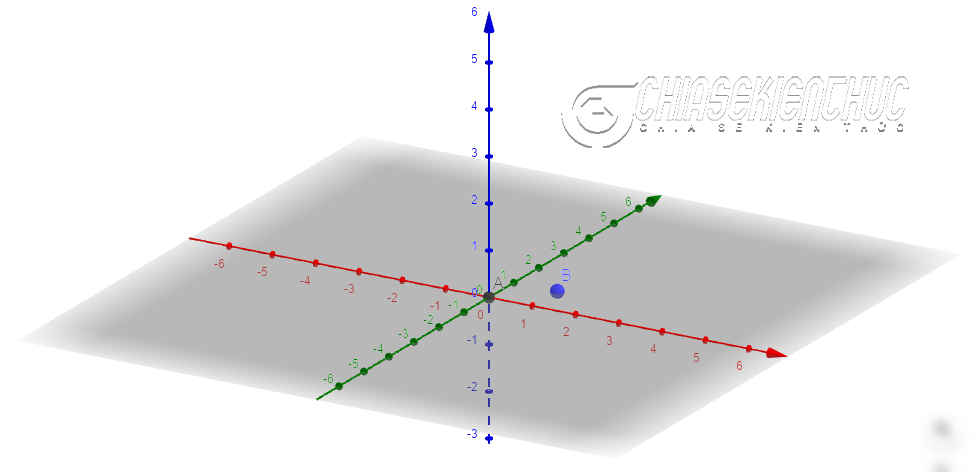
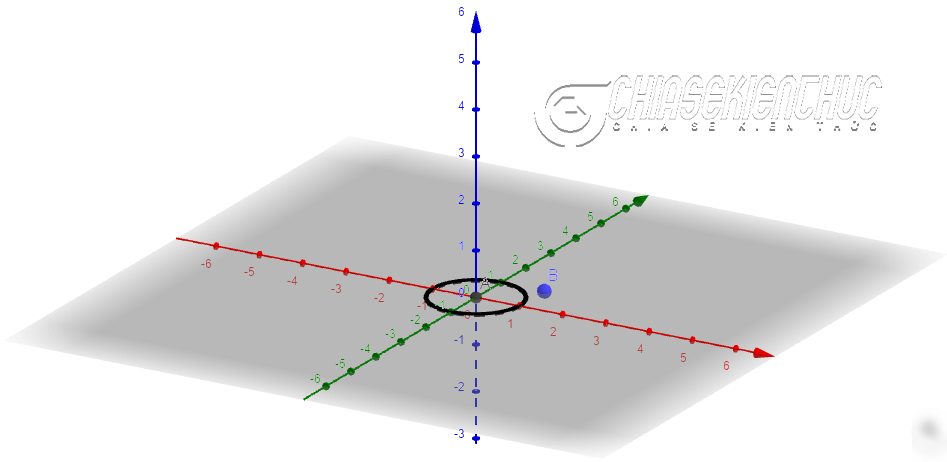
+ Bước 2: Dựng hai điểm A và B, vị trí của A và B có thể khác với vị trí trong bài viết, nhưng bạn nên tạo sao cho chúng đều nằm trên mặt phẳng Oz

Thực hiện: Chọn công cụ Point => di chuyển chuột đến vị trí thích hợp rồi nháy chuột để tạo điểm A và B

+ Bước 3: Bây giờ chúng ta sẽ dựng đường tròn biết tâm, bán kính và hướng. Cụ thể như sau:

Đường tròn này sẽ nằm trên mặt phẳng Oz.
Vì bán kính là a nên GeoGera sẽ tự động tạo ra một thanh trượt. Khi muốn thay đổi bán kính của đường tròn ta chỉ cần kéo thả thanh trượt này là được.

Thực hiện: Chọn công cụ Circle with Center, Radius and Direction => chọn điểm A => chọn điểm B => nhập bán kính là a => chọn Create Sliders.

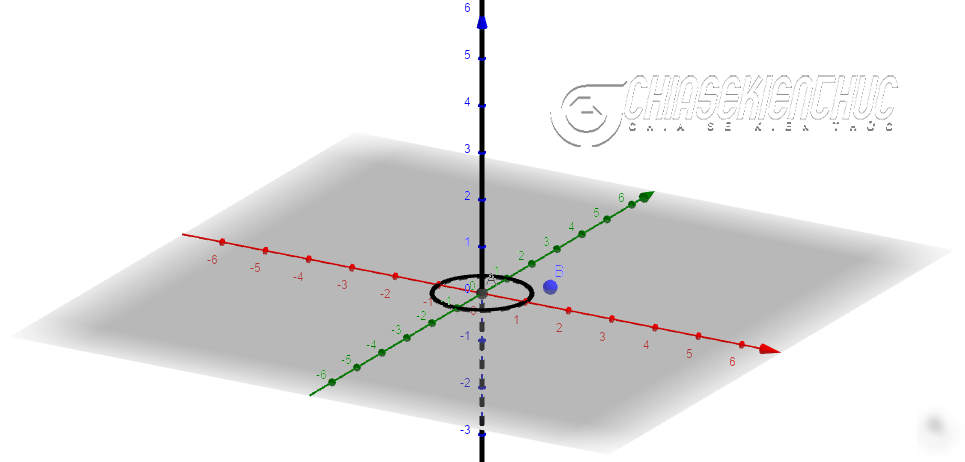
+ Bước 4: Dựng đường thẳng đi qua A và vuông góc với mặt phẳng. Từ đây về sau nếu không có nói gì thêm thì chúng ta sẽ hiểu mặt phẳng ở đây là mặt phẳng mặc định của phần mềm.

Thực hiện: Chọn công cụ Perpendicular Line => chọn điểm A => chọn mặt phẳng.

+ Bước 5: Dựng một điểm bất kì thuộc đường tròn (dựng điểm C). Chọn công cụ Point on Object => nháy chuột vào một vị trí bất kì trên đường tròn.

+ Bước 6: Dựng đoạn thẳng AC. Chọn công cụ Segment => chọn điểm A => chọn điểm C

+ Bước 7: Dựng đường thẳng đi qua C vuông góc với mặt phẳng. Chọn công cụ Perpendicular Line => chọn điểm C => chọn mặt phẳng.

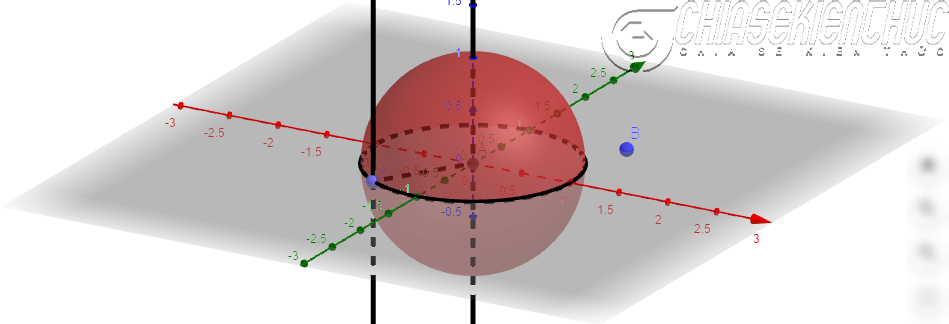
+ Bước 8: Dựng hình cầu tâm A, bán kính a

Trong thức tế, khi thiết kế bạn nên nhập bán kính là 2a. Bởi nếu nhập là a chúng ta sẽ tạo ra một hình chữ nhật đặc biệt (hình vuông), dễ gây ngộ nhận cho học sinh.

Thực hiện: Chọn công cụ Sphere: Center & Radius => chọn điểm A => nhập bán kính là a

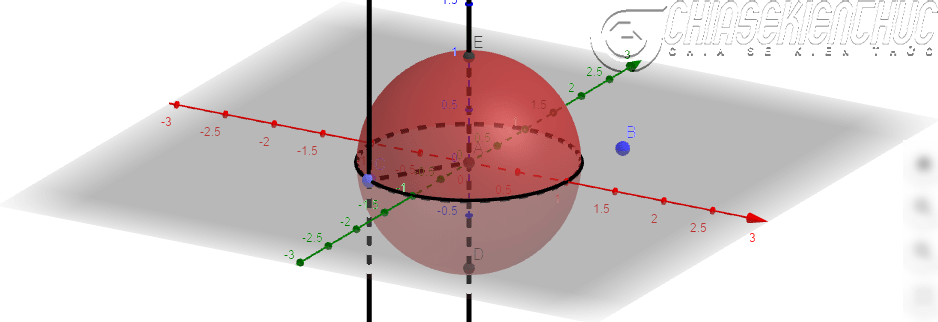
+ Bước 9: Dựng giao điểm của hình cầu với đường thẳng – đường thẳng đi qua điểm A và vuông góc với mặt phẳng (dựng điểm E, D)

Thực hiện: Chọn công cụ Intersect => chọn hình cầu => chọn đường thẳng.

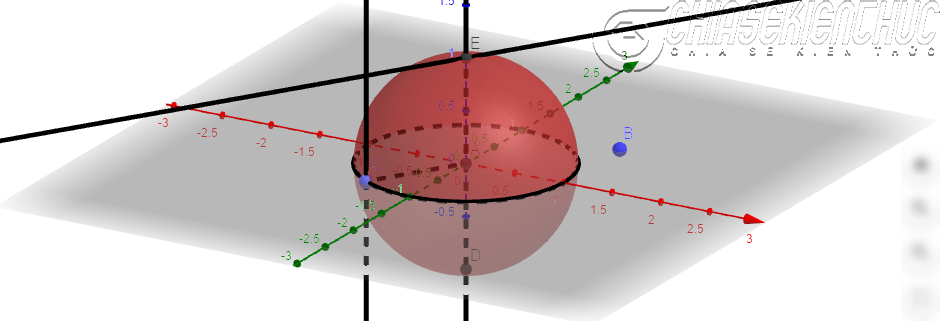
+ Bước 10: Dựng đường thẳng đi qua điểm E song song với đoạn thẳng AC. Chọn công cụ Parallel Line => chọn E => chọn AC

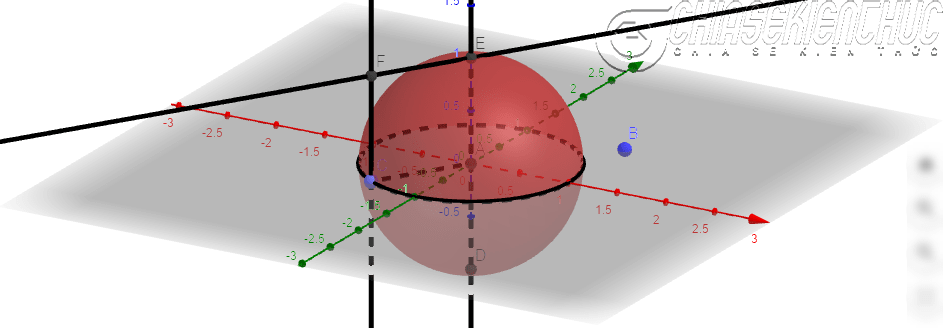
+ Bước 11: Dựng giao điểm của đường vừa dựng với đường thẳng – đường thẳng đi qua C vuông góc mặt phẳng (dựng điểm F)

Thực hiện: Chọn công cụ Intersect => chọn vào đường thằng => chọn vào đường thẳng.

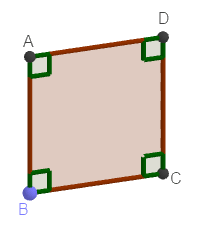
+ Bước 12: Dựng hình chữ nhật FEAC. Chọn công cụ Polygon => chọn lần lượt bốn điểm F, E, A, C.

+ Bước 13:

Tùy chọn ẩn các đối tượng phụ (điểm B, D, hình cầu, đoạn thẳng AC, các đường thẳng, …) và các đối tượng không cần thiết (mặt phẳng, hệ trục tọa độ)
Đổi tên các điểm
Sử dụng công cụ Angle để đánh dấu góc.

NOTE: Như mình đã nói ở trên, những thao tác này mình đã hướng dẫn chi tiết trong nhiều bài viết rồi, nên bài này mình sẽ không hướng dẫn lại nữa nhé các bạn !

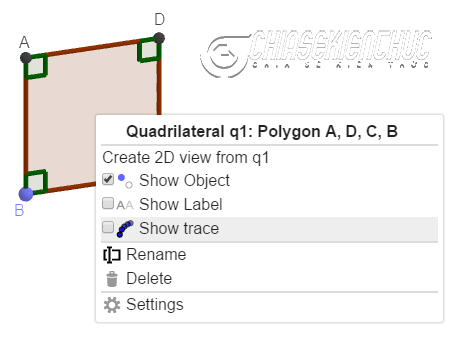
+ Bước 14: Tạo vết cho hình chữ nhật ABCD. Nháy chuột phải vào hình chữ nhật ABCD => chọn Show trace

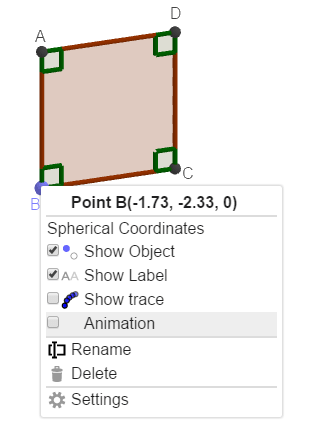
+ Bước 15: Tạo hiệu ứng chuyển động cho hình chữ nhật ABCD. Nháy chuột phải vào điểm B => và chọn Animation

Ngay khi chọn vào Animation thì hình chữ nhật ABCD sẽ quay quanh CD. Và khi ABCD quay quanh CD đúng một vòng chúng ta sẽ thu được hình trụ.

Muốn dừng hiệu ứng lại bạn hãy chọn vào điểm B => bỏ chọn Animation

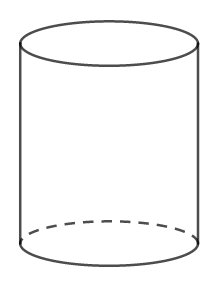
#3. Vẽ hình trụ trong không gian 3 chiều

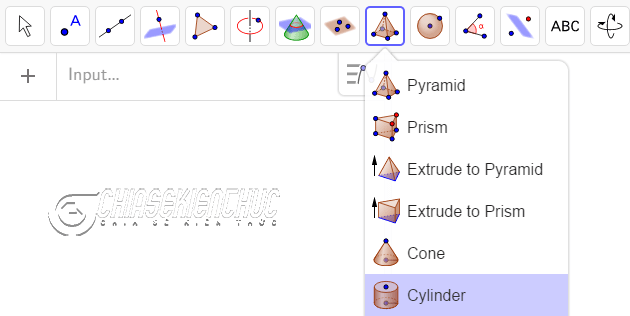
Trong trường hợp bạn chỉ cần vẽ hình trụ để minh họa thì bạn có thể sử dụng công cụ Cylinder. Các bước vẽ cụ thể

+ Bước 1: Chọn vào công cụ Cylinder

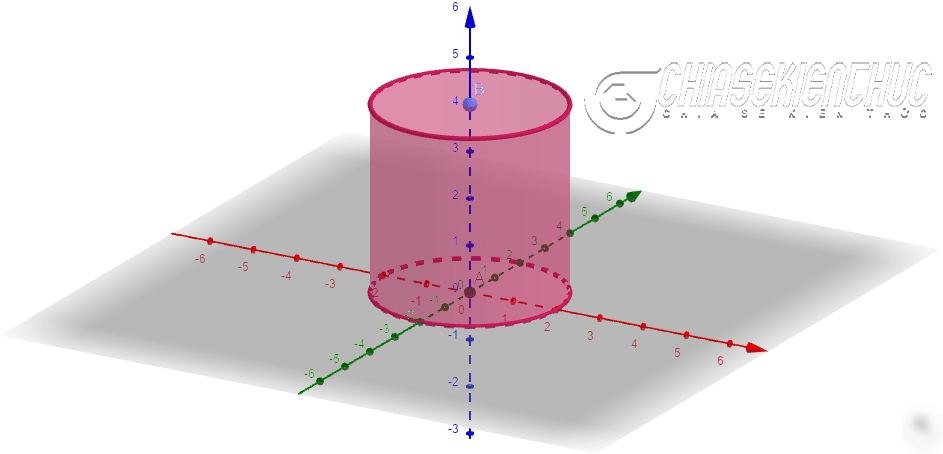
+ Bước 2: Nháy chuột để dựng hai điểm A và B (vị trí bất kì) trong không gian => nhập bán kính => chọn OK

#4. “Vẽ hình trụ trên mặt phẳng”

Nhiều trường hợp chúng ta cần vẽ hình trụ trên mặt phẳng, chẳng hạn như trong các đề kiểm tra, đề thi, …

Trong thực tế thì không thể có chuyện này được, một hình thuộc không gian không thể thuộc mặt phẳng. Vì vậy người ta thường gọi nôm na mặt phẳng này là mặt phẳng 2.5 chiều

Các bước vẽ cơ bản:

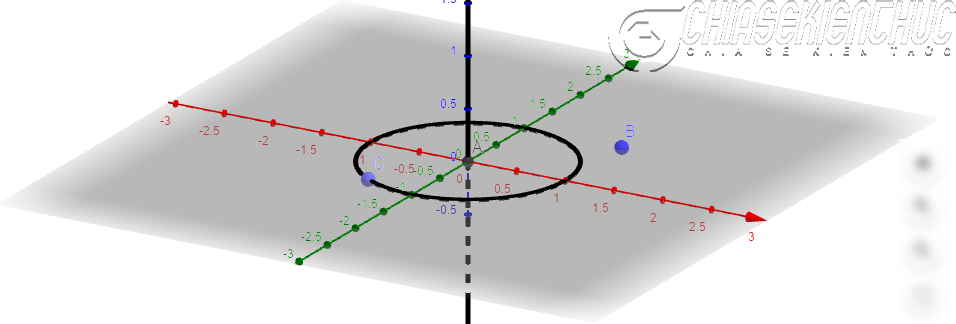
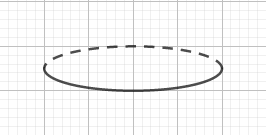
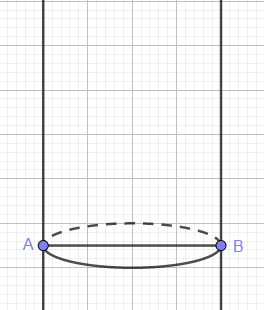
+ Bước 1: Dựng hình Ellipse với nửa trên là nét đứt. Nếu chưa biết cách làm thì bạn hãy xem cách vẽ trong bài viết Ứng dụng phần mềm GeoGebra trong việc dạy Toán học

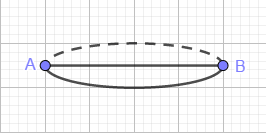
+ Bước 2: Dựng hai điểm A và B có vị trí như hình => dựng đoạn thẳng AB

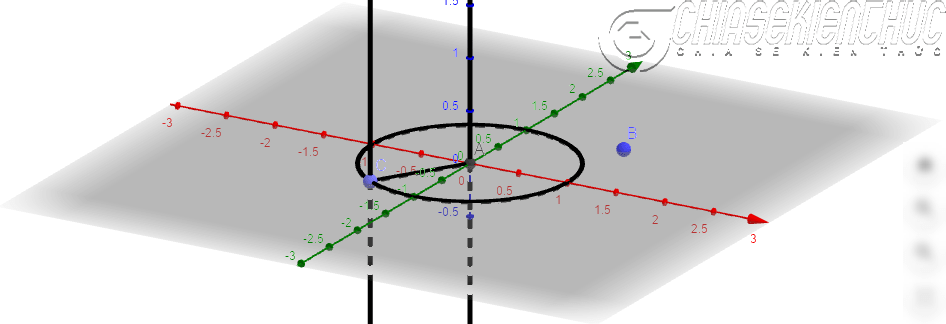
+ Bước 3: Dựng đường thẳng đi qua A vuông góc AB => dựng đường thẳng đi qua B vuông góc AB

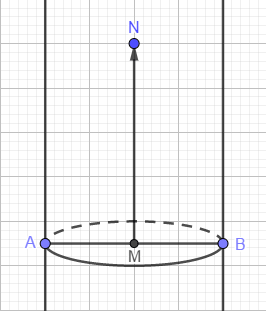
+ Bước 4: Dựng điểm M (M là trung điểm AB) => dựng điểm N (N có vị trí như hình) => dựng Vecto MN

+ Bước 5: Tịnh tiến Ellipse theo Vecto MN => tùy chỉnh ẩn các đối tượng phụ, các đối tượng không cần thiết và định dạng lại.

#5. Lời kết

Vâng, như vậy là mình đã vừa hướng dẫn xong cho các bạn cách mô hình hóa khái niệm hình trụ bằng phần mềm GeoGebra rồi ha.

Như đã giới thiệu trong những bài viết trước, sau khi thiết kế xong mô hình bằng GoeGebra thì bạn có thể:

Nhúng trực tiếp nó vào PowerPoint (không khuyến khích).
Sử dụng các phần mềm quay video màn hình để chuyển nó thành *.mp4
Mở rồi thực hiện trực tiếp trên phần mềm GeoGebra.
Sử dụng phần mềm SnagIT để chuyển nó thành ảnh động GIF.

Cá nhân mình khuyến khích các bạn nên sử dụng phần mềm SnagIT để chuyển nó thành ảnh động => rồi chèn vào PowerPoint. Đây có lẽ là cách tối ưu nhất trong thời điểm hiện tại.

Ngoài ra thì bạn có thể tải tệp tin nguồn *.ggb tại đây hoặc tại đây. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com